Rank-N-Contrast
Learning Continuous Representations for Regression
Rank-N-Contrast: Learning Continuous Representations for Regression
This project reproduces the NeurIPS 2023 Spotlight paper Rank-N-Contrast: Learning Continuous Representations for Regression as a course project for CS F425 - Deep Learning. Rank-N-Contrast (RNC) is a novel framework that learns continuous representations for regression by contrasting samples against each other based on their rankings in the target space.
Key Concept
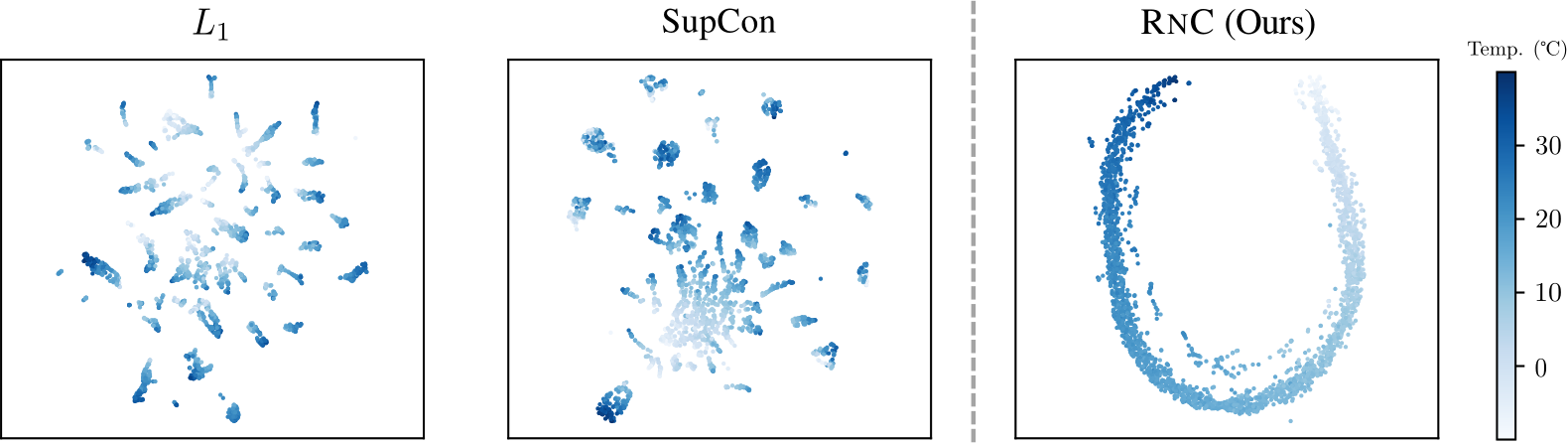
Traditional regression models typically learn in an end-to-end fashion without explicitly emphasizing a regression-aware representation. This leads to fragmented representations that fail to capture the continuous nature of sample orders. RNC addresses this limitation by learning representations that preserve the ordering relationships between samples according to their target values.
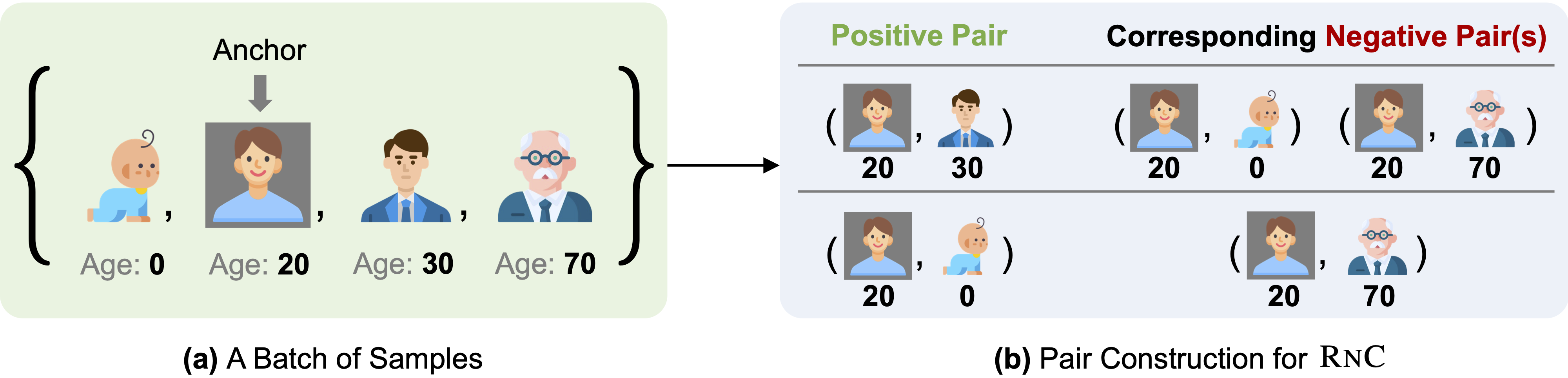
The RnC Loss Function
The core of our implementation is the RnC Loss function that ranks samples in a batch according to their labels and then contrasts them against each other based on their relative rankings:
from loss import RnCLoss
# define loss function with temperature, label difference measure, and feature similarity measure
criterion = RnCLoss(temperature=2, label_diff='l1', feature_sim='l2')
loss = criterion(features, labels) # features: (bs, 2, fear_dim), labels: (bs, label_dim)
Experiments and Results
We conducted experiments in two domains:
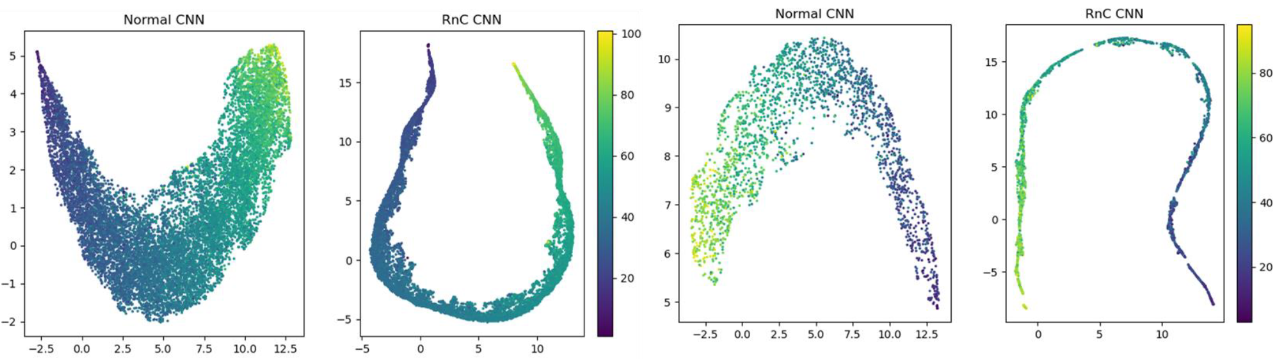
1. Computer Vision: Age Estimation
We reproduced the original paper’s results using the AgeDB dataset, which contains face images of celebrities, politicians, and scientists at different ages (ranging from 3 to 101 years).

Our implementation follows a two-stage approach:
- Train an encoder with the RnC framework
- Use the trained encoder to train a regressor on top
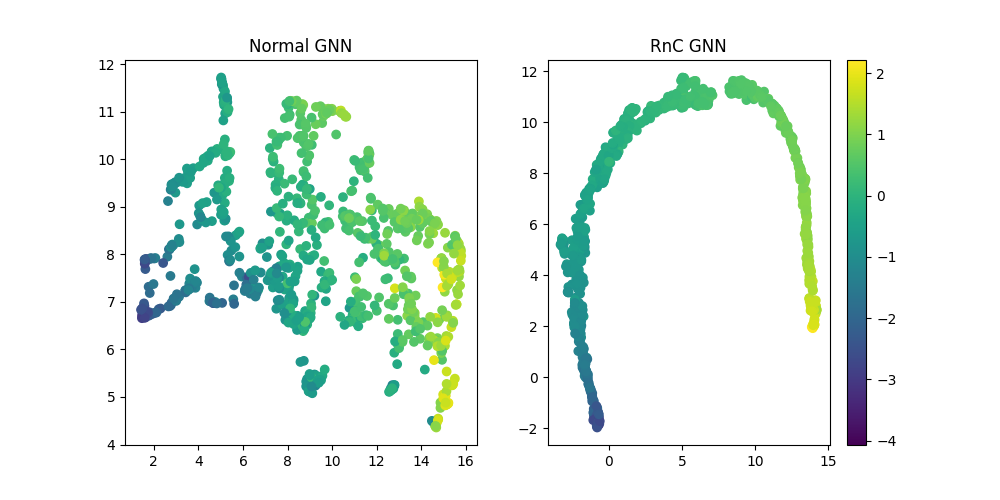
2. Graph Regression: ESOL Dataset
We extended the original work by applying RNC to a graph regression task using the ESOL dataset (water solubility prediction for molecules).
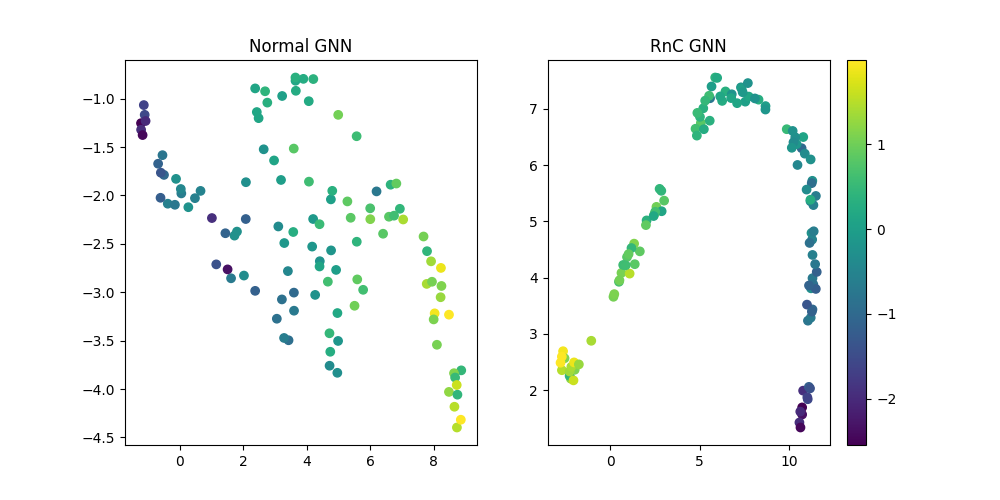
Our results demonstrate the superiority of RNC over standard regression approaches:
| Method / Loss | test MAE | test RMSE | test MSE | validation MAE | validation RMSE | validation MSE |
|---|---|---|---|---|---|---|
| normal-L1 | 0.247 | 0.326 | 0.106 | 0.224 | 0.325 | 0.106 |
| RnC(L1) + freeze | 0.219 | 0.297 | 0.088 | 0.255 | 0.359 | 0.129 |
| RnC(L1) | 0.212 | 0.314 | 0.099 | 0.235 | 0.345 | 0.119 |
| RnC(L2) | 0.266 | 0.342 | 0.117 | 0.276 | 0.366 | 0.134 |
| RnC(Huber) | 0.242 | 0.326 | 0.106 | 0.245 | 0.317 | 0.101 |
Key Findings
Our experiments revealed several intriguing properties of RNC:
- Better Performance: RNC consistently outperforms standard regression approaches across different tasks.
- Improved Data Efficiency: RNC requires less training data to achieve comparable performance.
- Enhanced Robustness: RNC shows better robustness to spurious targets and data corruptions.
- Better Generalization: RNC generalizes better to distribution shifts and unseen targets.
Conclusion
Our reproduction and extension of the Rank-N-Contrast framework demonstrate its effectiveness in learning continuous representations for regression tasks. By explicitly enforcing the ordering of samples in the representation space according to their target values, RNC creates more meaningful embeddings that lead to improved regression performance, robustness, and generalization.
This project showcases the potential of representation learning approaches for regression tasks and opens up new avenues for future research in this direction.